Sorting Network Verify and Draw

1. Introduction

This sorting network drawing and verification tool, the source code of which is written and maintained by Ian Parberry, can generate instances of common sorting networks or load them from a text file, display them in a window, and export the image to a file in bitmap or vector graphic formats.

A comparator network consists of a fixed number of channels that carry scalar values from some strongly ordered set (usually integers or floating point numbers), and comparators that connect pairs of channels, swapping the values on the channels if they are not in a desired order. Comparator networks that sort all inputs are called sorting networks. See the Wikipedia page for more information.

Comparator network are typically drawn with the channels running horizontally and the comparators running vertically. For example, Fig. 1 shows a 16-input sorting network. The comparators route the smaller of the values on its channels to the upper of the two channels that it is connected to, and the larger of the two values to the lower channel. A comparator network can be be tested to verify that it is a sorting network, that is, whether the outputs of the sorting network are in non-descending order from top to bottom.

Fig. 1: A 16-input sorting network.

The remainder of this page is divided into 3 sections. Section 2 gives an overview of the code. Section 3 describes the controls, which are contained in the menu bar. Section 4 lists the sample input files provided, each with a brief description.

---

2. Code Overview

It is assumed that the reader is familiar with the basics of Windows programming such as WinMain, the Window procedure, message passing, and drop-down menus. Main.cpp contains the mandatory Windows functions wWinMain() and a Window procedure WndProc(), which use a single global variable static CMain* g_pMain. Most of the other gnarly Windows-specific code, which used the Win32 API, is hidden away in WindowsHelpers.cpp and WindowsHelpers.cpp. Gdi+ is used for the graphics. The main class is CMain, which encapsulates the main body of the code in the approved object-oriented fashion.

---

3. The Controls

The menu bar at the top of the program window has four drop-down menus, File, Generate, View, and Help.

3.1 The File Menu

The File menu has four options, Open, Verify, Export, and Quit.

3.1.1 Open

Selecting Open will pop up an Open File dialog box that will allow you to choose a text file to load. Be aware that there is minimal error checking and no error reporting, so it is best to load only text files that are in the correct format for a comparator network, which is as follows. An \(n\)-input comparator network of depth \(d\) will have \(d\) lines of text, one for each layer of non-overlapping comparators (that is, no two comparators in the same level can have a channel in common). Each line contains a number of pairs \(i,j\) of channel numbers, one for each comparator on that level, where \(0 \leq i,j < n\). The channel numbers should be separated by spaces. For example, the following three-line text file

 0 1 2 3
 0 2 1 3
 1 2

describes the four-input sorting network below in Fig. 2 The channels are numbered 0 through 3 from bottom to top.

Fig. 2: A 4-input sorting network.

This sorting network can be loaded from w4d3s5.txt, which can be found, along with a few other examples, in the folder containing the Visual Studio solution file for this project.

3.1.2 Verify

Selecting Verify will pop up a dialog box that tells you various information about the current comparator network including its size and depth and whether it is a sorting network. This latter will take time exponential in the number of inputs, which is probably the best we can do because sorting network verification is Co-NP-complete even for shallow sorting networks (for example, see the following papers).

‍I. Parberry, "Single-exception sorting networks and the computational complexity of optimal sorting network verification", Mathematical Systems Theory, Vol. 23, No. 1, pp. 81–93, 1990.

I. Parberry, "On the computational complexity of optimal sorting network verification", in Parle91, Proceedings of Parallel Architectures and Languages Europe, pp. 252-269, 1991.

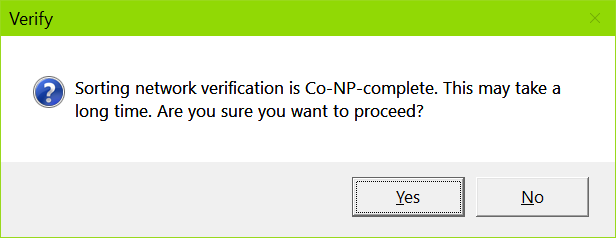
You will be warned if the number of inputs to the sorting network is 30 or larger via the following dialog box. Clicking on the No button will abort the test. Clicking on the Yes button will allow the test to proceed. Be aware that if it takes too long, then the only way to cancel it will be to quit the program by clicking several times on the standard red x button at top-right of the window.

If the comparator network is a sorting network, then any redundant comparators (those that do not perform any swaps when sorting) will be drawn in red, as shown in Fig. 3, the sorting network from file w10d7s32.txt.

Fig 3. A sorting network with a redundant comparator.

3.1.3 Export

The Export sub-menu will pop up a Save File dialog box that can save an image of the current comparator network in one of three formats.

1. Png saves the image as a bitmap in Portable Network Graphics format.
2. Svg saves the image in Scalable Vector Graphics format which can be opened in any web browser. This is superior to Png format in that it can be zoomed in or out without pixelation.
3. TeX saves the image as a \(\TeX\) picture environment that can be used as a figure in a \(\LaTeX\) document. For example, if the sorting network knuth16.txt is exported as knuth16.tex, then the following \(\LaTeX\) code will input it into a manuscript as a figure.

   \begin{figure}
     \centering\input{knuth16.tex}
     \caption{A 16-input sorting network.}
   \end{figure}

3.1.4 Quit

Selecting Quit will exit the program.

3.2 The Generate Menu

The Generate menu has six options, Bubblesort-min, Bubblesort-max, Bubblesort, Odd-even, Bitonic, and Pairwise. All of these will pop up a dialog box asking for the number of inputs.

3.2.1 Bubblesort-min

Bubblesort-min generates a sorting network that emulates the classical bubblesort algorithm by bubbling the smallest value to the minimum channel, then the second smallest value to the second minimum channel, etc., placing each sequence of comparators as close as possible to take advantage of parallelism. An \(n\)-input Bubblesort-min sorting network has depth \(2n-3\) and size (number of comparators) \(n(n-1)/2\). Fig. 4 (left) shows an example with 16 inputs.

Fig. 4: 16-input bubblesort-min (left), bubblesort-max (center) and bubblesort (right) sorting networks.

3.2.2 Bubblesort-max

Bubblesort-max generates a similar sorting network that bubbles maxima instead of minima. It also has depth \(2n-3\) and size \(n(n-1)/2\). Fig. 4 (center) shows an example with 16 inputs.

3.2.3 Bubblesort

Bubblesort generates a fully parallelized bubblesort. An \(n\)-input Bubblesort sorting network has depth \(n\) and size \(n(n-1)/2\). Fig. 4 (right) shows an example with 16 inputs.

3.2.3 Odd-even

Odd-even generates Batcher's odd-even sorting network from the following paper. Fig. 5 (left) shows an odd-even sorting network with 16 inputs.

‍K. E. Batcher, "Sorting networks and their applications", In Proc. AFIPS Spring Joint Computer Conference, Vol. 32, pp. 307–314, 1968.

Fig. 5: A 16-input odd-even (left), bitonic (center), and pairwise (right) sorting network.

3.2.4 Bitonic

Bitonic generates Batcher's bitonic sorting network from the following paper. Fig. 5 (center) shows a bitonic sorting network with 16 inputs.

‍K. E. Batcher, "Sorting networks and their applications", In Proc. AFIPS Spring Joint Computer Conference, Vol. 32, pp. 307–314, 1968.

3.2.5 Pairwise

Pairwise generates the pairwise sorting network from the following paper. Fig. 5 (right) shows a pairwise sorting network with 16 inputs.

‍I. Parberry, "The pairwise sorting network", Parallel Processing Letters, Vol. 2, No. 2,3, pp. 205-211, 1992.

3.2.6 On the Number of Inputs to Odd-even, Pairwise, and Bitonic Sorting Networks

Technically, the odd-even, bitonic, and pairwise sorting networks are only defined when the number of inputs is a power of 2. If you specify a number of inputs \(n\) that is not a power of 2, the generator will construct a sorting network with \(2^{\lceil \log_2 n\rceil}\) inputs (that is, it will round up to the next power of 2, if necessary) and remove unneeded channels and the comparators on them. If \(n\) is a power of 2, the odd-even and pairwise sorting networks have depth \(\log_2(n) (\log_2 (n) + 1)/2\) and size \(n\log_2 (n)(\log_2 (n) - 1)/4 + n - 1\), and the bitonic sorting network has the same depth and size \(n \log_2(n)/2\).

3.3 The View Menu

The View menu has three options, Horizontal, and Vertical. The default is Horizontal which displays and exports images in the standard form with horizontal channels and the output in non-decreasing order from bottom to top. Selecting Vertical will display and exports image with vertical channels and the output in non-decreasing order from left to right. For example, in Fig. 6 shows the 4-input sorting network from Fig. 2 drawn in vertical format.

Fig. 6: A 4-input sorting network drawn in vertical format.

3.4 The Help Menu

The Help menu has two entries, Display help which opens up this documentation in a browser, and About which displays the About dialog box.

---

4. Sorting Network Files

The repository contains 11 sample comparator network files. The input format is described in Section 3.1.1.

4.1 bad-input.txt

An example of a bad input file for testing purposes.

  0 1 2 3
  0 2 foo 3
  1 2

4.2 does-not-sort.txt:

A 16-input comparator network does not sort obtained from knuth16.txt below by deleting a comparator.

4.3 knuth16.txt

A 16-input sorting network of depth 9 and size 61 shown in Fig. 1.

4.4 w4d3s5.txt

A 4-input sorting network of depth 3 and size 5 shown in Fig. 2.

4.5 w5d5s8.txt

A 5-input sorting network of depth 5 and size 8.

4.6 w6d5s12.txt

A 6-input sorting network of depth 5 and size 12.

4.7 w7d6s16.txt

A 7-input sorting network of depth 6 and size 16.

4.8 w8d6s19.txt

An 8-input sorting network of depth 6 and size 19.

4.9 w9d7s27.txt

A 9-input sorting network of depth 7 and size 27.

4.10 w10d7s31.txt

A 10-input sorting network of depth 7 and size 31.

4.11 w10d7s32.txt

A 10-input sorting network of depth 7 and size 32 obtained by inserting a redundant comparator (shown in red in Fig. 3) into w10d7s31.txt above