Sorting Network Search

1. Introduction

A comparator network consists of a fixed number of channels that carry scalar values from some strongly ordered set (usually integers or floating point numbers), and comparators that connect pairs of channels, swapping the values on the channels if they are not in a desired order. Comparator networks that sort all inputs are called sorting networks. See the Wikipedia page for more information.

This sorting network backtracking code, the source code of which is written and maintained by Ian Parberry, can be used to search for sorting networks with a small number of inputs. Any sorting network found will be saved in the text format used by the sorting network viewer https://github.com/Ian-Parberry/sortingnetworkviewer, which can then be used to display them in a window and export the image to a file in bitmap or vector graphic formats.

This code implements the algorithm from

‍I. Parberry, "A computer assisted optimal depth lower bound for nine-input sorting networks", Mathematical Systems Theory, Vol. 24, pp. 101-116, 1991.

A preliminary version of this paper appeared in

‍I. Parberry, "A computer assisted optimal depth lower bound for nine-input sorting networks", Proceedings of Supercomputing '89, pp. 152-161, 1989.

A free PDF version can be found at https://ianparberry.com/pubs/9-input.pdf. It will henceforth be referred to in this documentation as the paper.

Over a quarter of a century later, these results were cleverly expanded up to 20 inputs using a SAT solver in

‍D. Bundala, M. Codish, L. Cruz-Filipe, P. Schneider-Kamp, J. Závodný, "Optimal-depth sorting networks", Journal of Computer and System Sciences, Vol. 84, pp. 185-204, 2017.

The original backtracking code from the 1980s has been lost to crashed floppy disks, hard drives and magnetic tapes. However, in the interest of completeness I have recreated it from the paper. Any errors in this code do not imply errors in the original 1980s version.

The remainder of this page is divided into three sections. Section 2 gives an overview of the code. Section 3 describes some experimental results, and Section 4 shows how to run the code.

---

2. Code Overview

This section is divided into four subsections. Section 2.1 describes how settings are shared through the code. Section 2.2 gives an overview of the hierarchy of sorting network classes used. Section 2.3 describes the multithreading classes. Section 2.4 puts together the classes described in the previous three subsections.

2.1 Shared Settings

CSettings, shares settings m_nWidth (the number of inputs, or width of the sorting networks to be searched for) and m_nDepth (the number of levels, or depth of the sorting networks to be searched for). It is a singleton class that enables us to share these values quickly and transparently by using it as a base class. The maximum width and depth are constrained by sensible maximum values in Defines.h.

2.2 Sorting Network Classes

Sorting networks are represented by members of a collection of derived classes as shown in Fig. 1.

Fig. 1: Annotated inheritance diagram.

Each of these will be described in a separate subsubsection below.

2.2.1 CComparatorNetwork

CComparatorNetwork represents a comparator network, that is, a network of comparators. It is derived from CSettings. Since the search will iterate through all matchings at all levels, there is a danger of including repeat comparators that are duplicates of comparators in the previous level. CComparatorNetwork contains code that removes repeat comparators, and also code for saving a comparator network to a text file in the format used by the sorting network viewer.

2.2.2 CSortingNetwork

CSortingNetwork represents a sorting network, that is, a comparator network that sorts all inputs. It is derived from CComparatorNetwork. The main new function here is CSortingNetwork::Sorts(), which returns true if the base comparator network sorts all inputs. This function uses the Zero-One Principle and a binary Gray code generator CBinaryGrayCode to generate the test inputs. The main functions here are CBinaryGrayCode::Initialize() to initialize to the first (all zero) binary string, and CBinaryGrayCode::Next() to generate the next binary string (which differs from the previous one in exactly one bit, the index of which is returned).

2.2.3 C1NF

C1NF represents a first normal form sorting network, which has comparators in the first level between channels 0-1, 2-3, 4-5, etc. It is derived from CSortingNetwork and has similar functionality, the most important modification being that C1NF::Sorts(), which overrides the virtual function CSortingNetwork::Sorts(), skips the first level and uses an instance of CTernaryGrayCode instead of CBinaryGrayCode to generate the inputs into the second level. Restricting our search to sorting networks in first normal form does no harm since every sorting network can be put into first normal form by permuting the channels and untwisting the comparators (see the paper).

2.2.4 CSearchable

CSearchable represents a searchable first normal form sorting network. It is derived from C1NF. The main function here is CSearchable::Backtrack, which iterates through all first normal form comparator networks of width CSettings::m_nWidth and depth CSettings::m_nDepth, and outputs those that sort all inputs. Functions FirstComparatorNetwork() and NextComparatorNetwork() are used to iterate through all levels from the second level down. These are then tested using the virtual function Sorts() which for CSearchable means C1NF::Sorts(), although this may be overridden in classes derived from it. Iteration over a given level is handled by a new matching generation algorithm derived from a permutation generation algorithm (see the paper), which for efficiency and clarity uses a second representation of a level in class CMatching. CMatching::Initialize() generates the first matching and CMatching::Next() generates the next. The map array CComparatorNetwork::m_nMatch is kept in step by calling CSearchable::SynchMatchingRepresentations() after each new matching is generated.

2.2.5 C2NF

C2NF represents a searchable second normal form sorting network. It is derived from CSearchable and has similar functionality. However, its second level is provided as a parameter. An instance of C2NF (or a class derived from it) will be given to a separate thread to test whether it can be built out into a sorting network.

2.2.6 CAutocomplete

CAutocomplete represents a searchable second normal form sorting network that constructs its last level (the one immediately before the outputs) instead of iterating through all possibilities. It is derived from C2NF. The last level is constructed using reachability, aborting if it is impossible to achieved in one level of comparators. Function CAutocomplete::StillSorts() is where this happens, overriding the much simpler two-line C1NF::StillSorts. See the paper for more details.

2.2.7 CNearsort

CNearsort represents a searchable second normal form sorting network that constructs its last level and prunes out at any second-from-last level that fails a reachability heuristic called nearsort. It is derived from CAutocomplete. If a comparator network is rejected at the second-from-last level by the nearsort heuristic, then it is guaranteed that there is no last level that completes a sorting network. See the paper for more details.

2.2.8 CNearsort2

CNearsort2 represents a searchable second normal form sorting network with nearsort that constructs its last level and prunes out at any third-from-last level that fails a reachability heuristic called nearsort2. It is derived from CNearsort. If a comparator network is rejected at the third-from-last level by the nearsort2 heuristic, then it is guaranteed that there are no last two levels that complete a sorting network. The nearsort2 heuristic was invented after the publication of the paper, however, it is the obvious extension of nearsort.

2.3 Multithreading

This code uses the thread++ library from https://github.com/Ian-Parberry/threadplusplus. We use a class CTask derived from CBaseTask in thread++, adding a pointer to an instance of CSearchable (or one of its derived classes) and an override CTask::Perform() for CBaseTask::Perform() that calls the virtual function CSearchable::Backtrack() or the appropriate overriding function. We also use a thread manager class CThreadManager derived from CBaseThreadManager in thread++. This provides a function CThreadManager::ProcessTask() that processes a task (an instance of CTask) by adding to a global count the number of sorting networks found from searching the instance of CSearchable pointed to by the task. Therefore, when all threads have terminated, CThreadManager::m_nCount contains the number of sorting networks found.

2.4 Tying It All Together

Function main() prompts the user for the width and depth of the sorting networks (subject to the maxima in Defines.h) and whether the new nearsort2 heuristic is to be used. It then creates a thread manager (an instance of CThreadManager) and passes it to function Search(). This function uses an instance of CLevel2Search to generate an std::vector<CMatching> of candidate matchings for the second level unique up to permutation of pairs of channels. See the paper for more details. For each second-level candidate an instance of C2NF, CAutocomplete, CNearsort, or CNearsort2 is created, wrapped up into an instance of CTask and inserted into the thread manager's task queue. Search() then uses the thread manager to spawn the threads, with until the threads have terminated, then call its function CBaseThreadManager::Process() to process the results (which calls CThreadManager::ProcessTask() for every processed task). The number of sorting networks found (which will have been output by the threads) is retrieved from the thread manager by calling the reader function CThreadManager::GetCount().

---

3. Experimental Results

The following experiments were run on an Intel® Core™ i9-7980XE CPU @ 2.60GHz running Windows 11.

Proving that there are no 9-input sorting networks of depth 6 took 1.75 seconds elapsed time consisting of 48 seconds CPU time over 35 threads, without using the new nearsort2 heuristic. Considering that the original computation in the 1980s described in the paper took over 200 hours of CRAY 2 time, this implies that my desktop computer is over 400,000 times faster than a 1980s supercomputer.

Proving that there are no 11-input sorting networks of depth 7 using the new nearsort2 heuristic took 2 days, 19 hr, 21 min sec elapsed time consisting of 88 days, 14 hr, 25 min CPU time over 35 threads using the new nearsort2 heuristic.

---

4. Using the Code

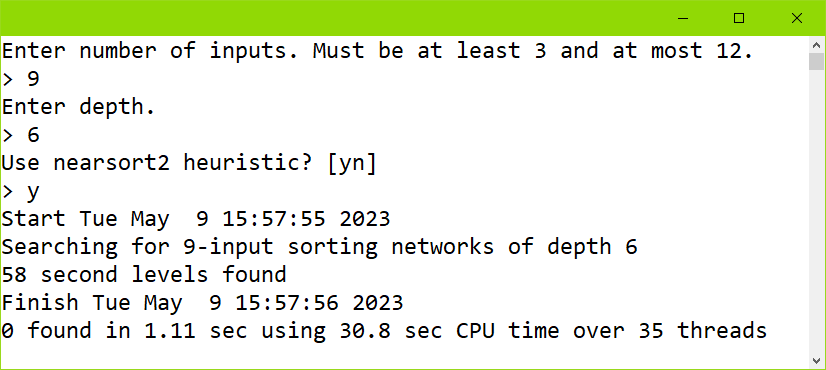
This project compiles into a console program that prompts the user for the number of inputs, the depth, and whether the new nearsort2 heuristic should be used. It reports the number of sorting networks found, the elapsed time, and the amount of CPU time summed over all threads (see Fig. 2). It also appends this data to a text file log.txt. A new text file level2-x.txt, where x is the number of channels, is created listing the level 2 candidate matchings.

Fig. 2: Console screen shot.