By the Numbers

Your Erdös number is defined as follows. Paul Erdös has Erdös number 0. If the smallest Erdös number of the coauthors of your research papers is i, then your Erdös number is i+1. My Erdös number is 3, at least four different ways:

1. Paul Erdös, Endre Szemerédi, Georg Schnitger, Ian Parberry
2. Paul Erdös, Jeff Shallit, John Sorenson, Ian Parberry
3. Paul Erdös, Carl Pomerance, John Sorenson, Ian Parberry
4. Paul Erdös, Michael Saks, Piotr Berman, Ian Parberry

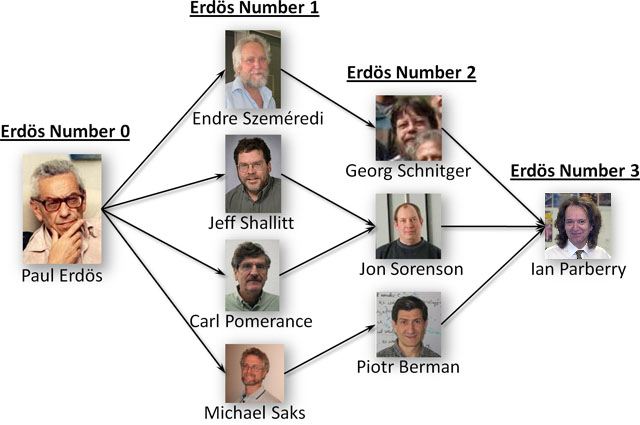
Citations for Erdös number 1:

1. Miklos Ajtai, Paul Erdös, Janos Komlós, and Endre Szemerédi, "On Turán's theorem for sparse graphs", Combinatorica, Vol. 1, No. 4, pp. 313-317, 1981.
2. Paul Erdös and Jeff Shallit, "New bounds on the length of finite Pierce and Engel series", Sém. Théor. Nombres Bordeaux (2) Vol. 3, no. 1, pp. 43-53, 1991.
3. Paul Erdös and Carl Pomerance, "On the largest prime factors of n and n+1" Aequationes Math., Vol. 17 no. 2-3, pp. 311-321, 1978.
4. Paul Erdös, Michael Saks, and Vera Sós,"Maximum induced trees in graphs", J. Combin. Theory Ser. B, Vol. 41, no. 1, 61-79, 1986.

Citations for Erdös number 2:

1. Wolfgang Maass, Georg Schnitger, Endre Szemerédi, and György Turán, "Two tapes versus one for off-line Turing machines", Computational Complexity, Vol. 3 , no. 4, pp. 392-401, 1993.
2. Piotr Berman, Avrim Blum, Amos Fiat, Howard Karloff, Adi Rosén, and Michael Saks, "Randomized robot navigation algorithms", Proceedings of the seventh annual ACM-SIAM symposium on Discrete algorithms, pp. 75-84, 1996.
3. Carl Pomerance and Jonathon Sorenson, "Counting the integers factorable via cyclotomic methods", Journal of Algorithms, Vol. 19, pp. 250-265, 1995.
4. Jeffrey Shallit and Jonathon Sorenson, "A binary algorithm for the Jacobi symbol", ACM SIGSAM Bulletin, Vol. 27, No. 1, Jan. 1993.

Citations for Erdös number 3:

1. Piotr Berman, Ian Parberry, and Georg Schnitger, "A Note on the Complexity of Reliability in Neural Networks", IEEE Transactions on Neural Networks, Vol. 3, No. 6, pp. 998-1002, 1992.
2. Jonathon Sorenson and Ian Parberry, "Two Fast Parallel Prime Number Sieves", Information and Computation, Vol. 114, No. 1, pp. 115-130, 1994.

Your Bacon number is defined as follows. Kevin Bacon has Bacon number 0. If the smallest Bacon number of the actors in movies in which you have acted is i, then your Bacon number is i+1. My Bacon number is 3 because I was an extra in the film Necessary Roughness which starred the actor Scott Bakula, who has Bacon Number 2 (you can check this using the Oracle of Bacon).

Your Erdös-Bacon Number is the sum of your Erdös number and your Bacon number. Very few people have a finite Erdös-Bacon number; Wikipedia lists just 9 scientists (not including me) and 5 actors. Since my Erdös number and my Bacon number are both 3, my Erdös-Bacon number is 6, putting me alongside luminaries such as the cosmologist Carl Sagan, physicists Richard Feynman and Stephen Hawking, and the actor Danica McKellar. I am not worthy.

• One of my papers is mentioned on p. 666 of the Second Edition of Knuth, vol. 3 .
• I'm 3 handshakes away from Abraham Lincoln: I've shaken the hand of a man (my father-in-law) who has shaken the hand of a man (a politician dunning for votes in rural West Virginia when my father-in-law was a kid) who claimed to have shaken the hand of Abraham Lincoln.